The absolute minimum - Find potential answers to this crossword clue at crosswordnexus.com. The Absolute Minimum Every Software Developer Absolutely, Positively Must Know About Unicode and Character Sets (No Excuses!) Top 10, New developer, News Ever wonder about that mysterious Content-Type tag? Find The Absolute Maximum And Absolute Minimum Values Of F On The Given Interval. Give Exact Answers Using Radicals, As Necessary. F(t) = T − T^1/3. −1, 3 Absolute Minimum Value Absolute Maximum Value 2. Find The Absolute Maximum And Absolute Minimum Values Of F On The Given Interval. F(x) = 2x3 − 3x2 − 72x + 1, Absolute Minimum Value.
The absolute minimum value of f(x) is: − 10 at x = − 2. The graph of f is shown below with the critical point and endpoints as well the absolute minimum and absolute maximum. Find the absolute maximum and minimum of function f defined by f(x) = 1 4x4 + 1. Absolute minimum definition: 1. The lowest value across a whole domain (= range) of a function: 2. The lowest value across a. Cambridge Dictionary +Plus.
| Derivatives: Min, Max, Critical Points.. |
| (Math | Calculus | Derivatives | Extrema/Concavity/Other) |
Asymptotes
Definition of a horizontal asymptote: The line y = y0 is a 'horizontal asymptote' of f(x) if and only if f(x) approaches y0 as x approaches + or - .Definition of a vertical asymptote: The line x = x0 is a 'vertical asymptote' of f(x) if and only if f(x) approaches + or - as x approaches x0 from the left or from the right.
Definition of a slant asymptote: the line y = ax + b is a 'slant asymptote' of f(x) if and only if lim (x-->+/-) f(x) = ax + b.
Absolute Min And Max Calc
ConcavityDefinition of a concave up curve: f(x) is 'concave up' at x0 if and only ifDefinition of a concave down curve: f(x) is 'concave down' at x0 if and only if
The second derivative test: If f
Local Minimum And Maximum
Critical PointsDefinition of a critical point: a critical point on f(x) occurs at x0 if and only if either f '(x0) is zero or the derivative doesn't exist.Extrema (Maxima and Minima)Local (Relative) Extrema
Definition of a local maxima: A function f(x) has a local maximum at x0 if and only if there exists some interval I containing x0 such that f(x0) >= f(x) for all x in I.
Definition of a local minima: A function f(x) has a local minimum at x0 if and only if there exists some interval I containing x0 such that f(x0) <= f(x) for all x in I.
Occurrence of local extrema: All local extrema occur at critical points, but not all critical points occur at local extrema.
The first derivative test for local extrema: If f(x) is increasing (

The second derivative test for local extrema: If
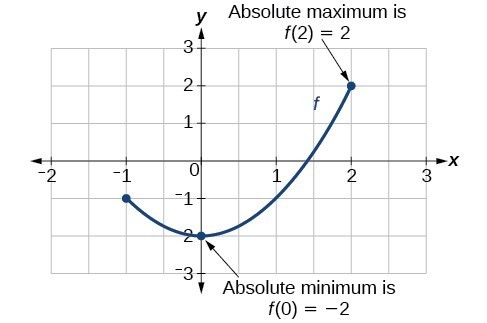
Absolute Extrema
Definition of absolute maxima: y0 is the 'absolute maximum' of f(x) on I if and only if y0 >= f(x) for all x on I.
Definition of absolute minima: y0 is the 'absolute minimum' of f(x) on I if and only if y0 <= f(x) for all x on I.
The extreme value theorem: If f(x) is continuous in a closed interval I, then f(x) has at least one absolute maximum and one absolute minimum in I.
Occurrence of absolute maxima: If f(x) is continuous in a closed interval I, then the absolute maximum of f(x) in I is the maximum value of f(x) on all local maxima and endpoints on I.
Occurrence of absolute minima: If f(x) is continuous in a closed interval I, then the absolute minimum of f(x) in I is the minimum value of f(x) on all local minima and endpoints on I.
Alternate method of finding extrema: If f(x) is continuous in a closed interval I, then the absolute extrema of f(x) in I occur at the critical points and/or at the endpoints of I.
(This is a less specific form of the above.) Newest citrix receiver.
Absolute Minimum Graph
0) > f(x) for all x in I to the left of x0 and f(x0) < f(x) for all x in I to the right of x0.Definition of a decreasing function: A function f(x) is 'decreasing' at a point x0 if and only if there exists some interval I containing x0 such that f(x0) < f(x) for all x in I to the left of x0 and f(x0) > f(x) for all x in I to the right of x0.
Jagged alliance 2 proedit download freerubackup. The first derivative test: If
Definition of an inflection point: An inflection point occurs on f(x) at x0 if and only if f(x) has a tangent line at x0 and there exists and interval I containing x0 such that f(x) is concave up on one side of x0 and concave down on the other side.
Find Absolute Minimum
